Sorting algorithm 모음
Insertion Sort (삽입 정렬)
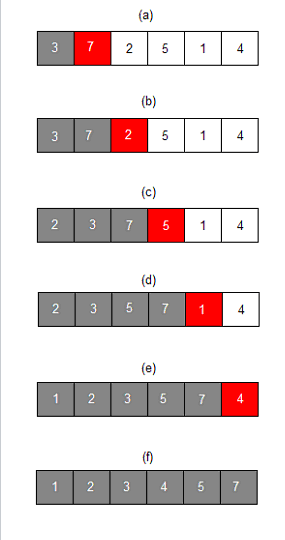
의사 코드

구현 코드
public class InsertionSort {
static void insertionSort(int[] input) {
int count = 0; // 반복 도는 횟수 확인
for (int j = 1; j < input.length; j++) {
count++;
int key = input[j];
int i = j - 1;
while (i > -1 && input[i] > key) {
count++;
input[i + 1] = input[i];
i -= 1;
}
input[i + 1] = key;
}
System.out.println(count);
}
public static void main(String[] args) {
// 30개 데이터로 테스트
// 최악의 경우 (내림차순 정렬된 배열)
int[] worstCase = {
30, 29, 28, 27, 26, 25, 24, 23, 22, 21,
20, 19, 18, 17, 16, 15, 14, 13, 12, 11,
10, 9, 8, 7, 6, 5, 4, 3, 2, 1
};
insertionSort(worstCase); //464
// 최상의 경우 (이미 정렬된 배열)
int[] bestCase = {
1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30
};
insertionSort(bestCase); //29
// 보통의 경우 (랜덤한 순서의 배열)
int[] averageCase = {
12, 5, 29, 7, 18, 23, 2, 25, 14, 8,
1, 27, 19, 3, 10, 30, 6, 22, 17, 4,
16, 24, 9, 11, 28, 15, 21, 26, 13, 20
};
insertionSort(averageCase); //218
}
}
시간 복잡도
- Best case : O(n)
- Worst case : O(n^2)
- Average case : O(n^2)
특징
- in-place sort : 추가 메모리 거의 없음
- stable sort : 같은 값의 순서가 유지됨.
- 작은 리스트 or 대체로 정렬된 경우 효율적
계속 추가
'algorithm' 카테고리의 다른 글
| 백준 1629번 문제 풀이(python) (1) | 2025.08.25 |
|---|---|
| 스트라센 알고리즘(Strassen Algorithm) - 행렬곱 (0) | 2025.03.02 |
| LeetCode Top Interview Questions - easy collection (0) | 2025.02.16 |
| 프로그래머스 21kakao_blind 순위검색(python) (2) | 2024.03.28 |
| 릿코드 2. Add Two Numbers, 49. Group Anagrams (0) | 2024.02.17 |
