기본 행렬곱

// pseudocode(의사코드)
for i from 1 to n: // A의 행(1부터 n까지)
for j from 1 to n: // B의 열(1부터 n까지)
C[i][j] = 0 // C의 각 원소 초기화
for k from 1 to n: // A의 열과 B의 행(k는 1부터 n까지)
C[i][j] = C[i][j] + A[i][k] * B[k][j]
end for
end for
end for행렬곱의 기본 연산은 중첩문이 3개로 O(n^3) 시간복잡도가 필요하다.
스트라센(Strassen) 행렬곱
스트라센 알고리즘은 분할 정복 방식을 사용하여 2개의 n x n 행렬 곱셈을 더 빠르게 계산한다.
가정) 행렬을 대칭적인 4개의 블록으로 분할한다.


일반적인 연산으로는 8번의 곱셈이 필요하다.
스트라센은 곱셈을 7번으로 줄이는 식을 만들었다.

처음에 행렬을 분할하여 A[i][j], B[i][j] 는 n/2 * n/2 행렬이다.
그래서 각각의 M은 n/2 * n/2 행렬곱으로 구성된다.
T(n) = n * n 행렬곱 이라할 때,
T(n/2) = n/2 * n/2 행렬곱이고

T(n/2)이 7번 있는 위와 같은 점화식을 얻을 수 있다.

n*n 행렬 덧뺄셈은 i와 j에 접근하는 for문 2개가 필요하므로 O(n^2) 이다.
스트라센 점화식에서 O((n/2)^2) ~= O(n^2) 으로 표기했다.
재귀 전개

점화식을 재귀적으로 전개해 보자.
T(n/2) = 7T(n/4) + O((n/2)^2)
T(n/4) = 7T(n/8) + O((n/4)^2)
....

재귀를 반복하면 다음과 같은 일반적인 형태가 보인다.
첫 번째 항과 두 번째 항을 각각 풀어보자.
재귀가 종료되는 시점은 n/(2^k) = 1, 즉 k = log2(n) 일 때이다. T(1) = O(1)
첫 번째 항
k를 대입하면

n = O(n)과 같으므로,
7^k = O(7^k) = O(n^log2(7)) 로 말할 수 있다.
두 번째 항
두 번째 항을 일반화하면 공비가 7/4 인 등비수열이다.

앞이 -4/3 이다. (시간 복잡도 점화식이 목표니까 크게 상관x)
첫 번째 항과 마찬가지로 k = log2(n)을 대입해 보자.


여기서 O 시간 복잡도는 주요 지배항 관점으로 바라보므로,
앞의 n^2 보다는 n^(log2(7/4) + 2)가 지배항이 된다. (같은 밑을 가진 거듭제곱의 곱셉에서 지수끼리는 값을 더한다.)
log2(7/4) + 2 = log2(7) - log2(4) + log2(4) 와 같으므로 n^(log2(7)) 로 정리된다.

그래서 두 번째 항도 O(n^log2(7)) 로 말할 수 있다.
최종
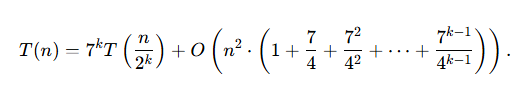
주어진 식의 두 항은 모두 O(n^log2(7))로 수렴하므로, 최종 시간 복잡도는 T(n) = O(n^log2(7)) 과 같다.
log2(7) = 2.80735... 으로
일반적인 행렬곱 시간복잡도 O(n^3) 에서 O(n^2.807..) 로 줄일 수 있었다.
스트라센 행렬곱 장단점
| 장점 | 단점 |
| O(n^2.81)로 시간 복잡도 개선 | 상수 계수가 높아 작은 행렬에서는 성능 저하 |
| 병렬화에 적합(분할 정복) | 부동소수점 연산에서 정확도 문제가 발생 가능 |
| 대형 행렬 계산에서 실질적인 성능 개선 | 더 많은 메모리 사용 |
| 현대 고속 알고리즘에 영감 | 비정사각형 행렬 처리의 추가 비용 |
후기
오랜만에 점화식을 따라가는 재미에 써봤다.
'algorithm' 카테고리의 다른 글
| 백준 1629번 문제 풀이(python) (1) | 2025.08.25 |
|---|---|
| Sorting Algorithm (0) | 2025.02.24 |
| LeetCode Top Interview Questions - easy collection (0) | 2025.02.16 |
| 프로그래머스 21kakao_blind 순위검색(python) (2) | 2024.03.28 |
| 릿코드 2. Add Two Numbers, 49. Group Anagrams (0) | 2024.02.17 |
